Topologia: Por que uma xícara é um donut

Imagine uma matemática com um superpoder peculiar. Diante dela, qualquer objeto pode ser esticado, amassado, torcido e deformado como se fosse feito de uma borracha infinitamente maleável. Há apenas duas proibições absolutas: não se pode rasgar nem colar partes novas. Sob esse olhar elástico, servir café da manhã vira um exercício filosófico. Uma xícara com alça e um donut tornam-se indistinguíveis — ambos têm exatamente um buraco. Já uma bola de sabão e um prato raso entram na mesma categoria: nenhum buraco. Esse é o ponto de vista da topologia.

A topologia é a matemática das propriedades qualitativas e estruturais que sobrevivem a deformações contínuas. Ela não se importa com medidas exatas, ângulos ou distâncias. Se a geometria tradicional é a arte de medir o mapa com régua e transferidor, a topologia é a disciplina que olha para o mesmo mapa e pergunta apenas: quantas peças há aqui? quantos buracos? o que está conectado a quê? É a ciência da forma em estado puro, despojada de tudo o que é acidental.

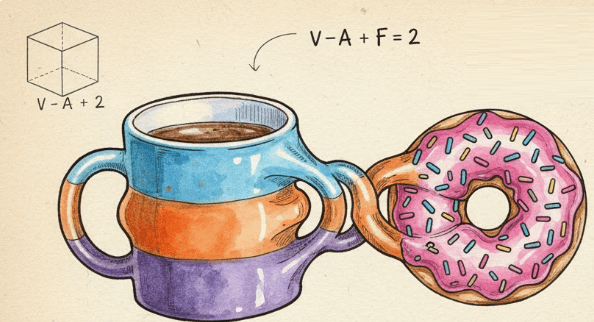
O contrato fundamental — a regra da borracha

No coração da topologia está a noção de homeomorfismo. Dois objetos são homeomorfos, ou topologicamente equivalentes, se um puder ser deformado continuamente no outro sem cortes nem colagens. É o grande nivelador das formas.

A galeria de transformações que isso permite parece mágica. Uma xícara pode amolecer, ter seu fundo empurrado para dentro, o corpo inflado e a alça engrossada até se tornar um toro — o sólido em forma de donut. Já transformar uma bola de futebol em um pneu de bicicleta é impossível: seria preciso abrir um furo na bola ou fechar o buraco do pneu, violando as regras. Até letras do alfabeto entram na brincadeira: um “C” e um “I” são essencialmente a mesma curva aberta; um “A”, um “P” e um “R” têm um buraco; um “B” tem dois.

O que a topologia faz, nesse jogo, é filtrar todos os detalhes métricos. O que sobra é o esqueleto de conectividade da forma.

Um dos primeiros instrumentos para capturar esse esqueleto foi a característica de Euler. No século XVIII, Leonhard Euler observou que, para qualquer poliedro que tenha a forma geral de uma bola, vale a relação V − A + F = 2 (vértices menos arestas mais faces). Um cubo dá 8 − 12 + 6 = 2. Um tetraedro, 4 − 6 + 4 = 2. Não importa o formato exato, mas a forma global: todos são, topologicamente, “esferas”.

Quando introduzimos um buraco — como no caso de um toro, o donut — o número muda. Para essa classe de superfícies, V − A + F = 0. A característica de Euler é um invariante topológico: um número que não muda sob deformações permitidas e que revela a qual “família” de formas um objeto pertence. É a essência da forma capturada em uma conta simples.

A terra dos fenômenos estranhos — onde a intuição falha

Se a topologia começa parecendo um jogo curioso com massas de modelar, logo ela nos conduz a objetos que desafiam profundamente o senso comum.

A fita de Möbius nasce de um experimento quase infantil: pegue uma tira de papel, dê meia-volta e cole as pontas. O resultado é uma superfície com propriedades desconcertantes. Uma formiga pode percorrer toda a faixa e visitar o que pareceriam ser “os dois lados” sem nunca cruzar uma borda — porque, topologicamente, há apenas um lado. A faixa tem também uma única borda contínua. E, se a cortarmos ao meio no sentido do comprimento, não obtemos duas tiras, mas uma única faixa maior, com duas voltas. O objeto mostra que as propriedades globais de uma superfície podem ser radicalmente diferentes do que sua aparência local sugere.

A garrafa de Klein leva essa estranheza adiante. Ela é, por assim dizer, a tentativa de criar uma superfície fechada — sem bordas — que seja não orientável como a faixa de Möbius. O preço é alto: para representá-la, a superfície precisa atravessar a si mesma no nosso espaço tridimensional. Em certo sentido, a garrafa de Klein só “existe” sem interseções em quatro dimensões. A lição é clara: a topologia lida com regras de conexão, não com as limitações de nossa visualização cotidiana.

O pensamento estrutural — a filosofia por trás da flexibilidade

A topologia costuma ser chamada de “geometria da folha de borracha”. O contraste com a geometria euclidiana é direto. Onde a geometria pergunta “quanto mede este segmento?” ou “qual é a medida deste ângulo?”, a topologia pergunta “isso forma um laço fechado?” ou “este espaço é todo de uma peça só?”. É uma mudança de foco: do quantitativo para o qualitativo.

Para classificar formas, os topólogos desenvolveram um verdadeiro arsenal de invariantes além da característica de Euler: grupo fundamental, grupos de homologia, entre outros. Eles funcionam como exames diagnósticos. Assim como um médico não vê diretamente uma doença, mas interpreta sinais e resultados de testes, o topólogo não “vê” a forma em si, mas infere sua estrutura a partir de invariantes que não mudam sob deformações.

Esse modo de pensar transbordou da matemática pura para várias áreas. Na física teórica, ideias topológicas aparecem na descrição da forma global do universo e em teorias que envolvem dimensões extras. Na ciência de dados, a Análise Topológica de Dados busca buracos, túneis e cavidades em nuvens de pontos de alta dimensão, revelando padrões estruturais invisíveis a métodos tradicionais. Na biologia, a topologia ajuda a entender o enovelamento do DNA e a estrutura tridimensional de proteínas.

A beleza do despojamento

Dizer que uma xícara é um donut não é uma piada interna de matemáticos; é a expressão de uma mudança radical de perspectiva. A topologia ignora material, tamanho, espessura e função. Interessa-se apenas pela arquitetura fundamental da conexão. Nesse nível mais profundo, ambos têm um único buraco.

A lição filosófica é ampla. A topologia nos treina a buscar propriedades estáveis em meio a transformações contínuas, a pensar qualitativamente antes de quantitativamente, a distinguir o essencial do acidental. É a matemática da resiliência estrutural.

Da próxima vez que você segurar uma xícara ou morder um donut, pode lembrar: ali há um pequeno teorema cotidiano. Um lembrete de que, no reino das formas puras, a aparência engana — e que, por trás de objetos tão diferentes, pode haver a mesma forma eterna sobrevivendo a todas as deformações imagináveis.